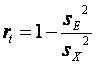 (3.8.1)
(3.8.1)Важнейшей характеристикой теста является его надежность, определяющая воспроизводимость результатов тестирования, их точность. Допустим, у нас есть гипотетическая группа испытуемых, которые немедленно забывают содержание теста по его завершении. Тогда, в случае надежного теста, повторяя тестирование многократно, мы должны получать одни и те же индивидуальные баллы. Для малонадежного теста результаты будут меняться каждый раз.
Тест представляет собой систему заданий. Качество заданий определяет надежность теста в целом. Рассмотрим пример. Допустим, тест состоит из заданий в закрытой форме, в которых по ошибке не указанные правильные ответы. Слабые испытуемые, не зная ответа, будут пытаться его угадать. Сильные испытуемые, зная верный ответ, но не находя его среди предложенных, так же вынуждены будут случайным образом выбирать любой из ответов. В итоге, индивидуальные баллы будут представлять собой случайные последовательности, не повторяющиеся в разных сеансах тестирования. Воспроизводимость тестовых баллов будет полностью отсутствовать и надежность теста будет близка к нулю. Низкая надежность теста обусловлена низким качеством тестовых заданий.
Для определения надежности реальных тестов можно использовать коэффициент корреляции Пирсона для индивидуальных баллов разных сеансов тестирования. Для организации разных сеансов тестирования можно использовать либо параллельные тесты, либо повторное тестирование через определенный промежуток времени. Можно также использовать результаты одного сеанса тестирования. При этом выполняют расщепление теста, например, на четные и нечетные задания и, затем, находят корреляцию между этими двумя половинами.
Надежность теста определяется разными методами. Рассмотрим их.
Из классической теории теста следует, что надежность теста есть
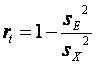 (3.8.1)
(3.8.1)
где SE2 - дисперсия ошибочного вклада тестовый балл, SE2 - дисперсия наблюдаемого тестового балла.
Когда ошибка отсутствует, коэффициент надежности равен единице. Если измеренный тестовый балл полностью обусловлен ошибкой измерения, то надежность теста равна нулю.
Ошибка измерения зависит от надежности теста rt.
![]() (3.8.2)
(3.8.2)
В работе13 показано, что корреляция rjT j-го задания с истинными тестовыми баллами T связана со средним значением его корреляции с другими заданиями теста7
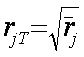 (3.8.3)
(3.8.3)
Если тест содержит задания с высокой внутренней корреляцией, то он будет высоко надежным и ошибка измерений будет низкой.
Определение надежности теста необходимо выполнять на специально подобранной выборке испытуемых, репрезентативно представляющей всю генеральную совокупность. Выборка должна быть достаточно большой - 200-300 человек. Чем больше выборка, тем точнее определяется надежность теста.
Для вычисления надежности теста нужны результаты двух испытаний, которые организуются следующими способами:
1-й способ – тестирование с помощью двух параллельных тестов (parallel-form reliability);
2-й способ – повторное тестирование с помощью одного и того же теста (test-retest reliability);
3-й способ – расщепление теста (split-half method).
Первый способ, пожалуй, самый лучший, с точки зрения расчета надежности. Основной проблемой здесь является разработка параллельных тестов. Крайне сложно создать тесты параллельные и по содержанию и по результатам. Ранее нами приводился пример «параллельных» заданий, дающих разные результаты:
6 + 3 = ____; 6 + ___ = 9; ___ + 3 = 9.
Второй способ технически гораздо проще, однако здесь появляются новые факторы.
Во-первых, первое тестирование изменяет уровень подготовленности испытуемых. Это может произойти по разным причинам, в частности, запоминание заданий теста. Поэтому повторное тестирование необходимо проводить спустя некоторый интервал времени. Этот интервал должен быть как можно больше.
Во-вторых, к моменту повторного тестирования изменяются внешние условия – другие социальная среда, другие взаимодействия с членами микросоциальной группы, другое время года, и т.д. Кроме того, изменились и сами испытуемые, изменился их уровень знаний как специальных, так общекультурных. В результате повторное тестирование проводится в иных условиях и иной группе испытуемых. В этой связи желательно временной интервал между тестированиями выбирать как можно короче. Мы получили взаимоисключающие требования к интервалу повтора тестирования, следовательно, здесь придется идти на компромисс. Можно рекомендовать интервал в один месяц, хотя подобные рекомендации должны подтверждаться экспериментально.
Надо осознавать, что повторное тестирование в силу указанных причин, в принципе не позволяет получить параллельные результаты даже для идеального теста с надежностью равной единице.
Третий способ очень прост. На основании всего лишь одного тестирования мы можем оценить надежность теста. Полученные результаты тем или иным способом делятся на две группы. Например, в первую входят результаты по четным заданиям, во вторую – результаты по нечетным заданиям. Затем вычисляется коэффициент корреляции между этими группами. Недостаток этого способа обусловлен неидентичностью этих групп.
В качестве примера проанализируем надежность четырех гипотетических тестов, выполненных на одной и той же выборке испытуемых (таблица 3.8.1).
Таблица 3.8.1. Индивидуальные баллы по четырем тестам.
|
|
Тест 1 |
|
Тест 2 |
|
Тест 3 |
|
Тест 4 |
||||
|
ФИО |
Х1 |
Х2 |
|
Х1 |
Х2 |
|
Х1 |
Х2 |
|
Х1 |
Х2 |
|
1 |
80 |
80 |
|
80 |
70 |
|
80 |
70 |
|
80 |
20 |
|
2 |
70 |
70 |
|
70 |
80 |
|
70 |
20 |
|
70 |
30 |
|
3 |
60 |
60 |
|
60 |
60 |
|
60 |
40 |
|
60 |
40 |
|
4 |
50 |
50 |
|
50 |
50 |
|
50 |
80 |
|
50 |
20 |
|
5 |
40 |
40 |
|
40 |
20 |
|
40 |
20 |
|
40 |
35 |
|
6 |
30 |
30 |
|
30 |
30 |
|
30 |
45 |
|
30 |
45 |
|
7 |
20 |
20 |
|
20 |
30 |
|
20 |
50 |
|
20 |
80 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rt |
1.00 |
|
rt |
0,884 |
|
rt |
0,101 |
|
rt |
-0,769 |
Испытуемых – 7 человек. Каждый тест проводился два раза, индивидуальные баллы испытуемых приведены в столбцах Х1 и Х2.
В последней строке приведены значения надежности теста (коэффициента корреляции Пирсона для совокупностей Х1 и Х2).
Тест 1. Индивидуальные баллы полностью совпадают. Надежность теста rt=1. Это идеальный случай, на практике не достижим.
Тест 2. Индивидуальные баллы различные, но наблюдается некоторое согласие. Большим и малым значениям Х1 приблизительно соответствуют большие и малые значения Х2. Тест обладает довольно высокой надежностью rt=0,884.
Тест 3. Между результатами обоих тестирований отсутствует какая-либо связь. Надежность теста низкая ( rt=0,101), тест непригоден к использованию.
Тест 4. Между результатами обоих тестирований есть довольно сильная, но отрицательная корреляция (rt= -0,769). Такой тест также нельзя использовать.
Тест можно использовать, если его коэффициент надежности не менее +0,7.
Приведем формулу для расчета коэффициента надежности при двукратном тестировании (параллельном или повторном)
 (3.8.4)
(3.8.4)
Xi и Yi– индивидуальные баллы i-го испытуемого в первом и во втором тестированиях; N –количество испытуемых;
На рис.3.8.1 приведена графическая интерпретация полученных коэффициентов надежности всех четырех тестов.
Рассмотрим теперь пример вычисления надежности теста методом расщепления. Используем бинарную матрицу из таблицы 3.2.5. Уберем из нее старые номера заданий и испытуемых (таблица 3.7.2).
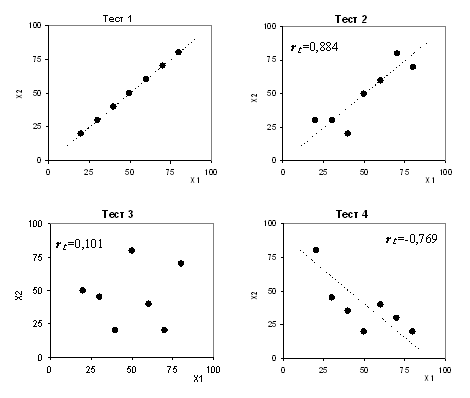
Рис.3.8.1. Графическая интерпретация надежности теста.
Таблица 3.8.2. бинарная матрица 10х8.
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Xi |
Чет. |
Нечет. |
|---|---|---|---|---|---|---|---|---|---|---|---|
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
7 |
3 |
4 |
|
2 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
6 |
4 |
2 |
|
3 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
6 |
3 |
3 |
|
4 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
5 |
2 |
3 |
|
5 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
4 |
1 |
3 |
|
6 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
3 |
1 |
2 |
|
7 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
2 |
1 |
1 |
|
8 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
2 |
1 |
1 |
|
9 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
|
10 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
В последних столбцах таблицы приведены индивидуальные баллы по четным и нечетным заданиям. Например, для испытуемого №1 количество верных ответов в четных заданиях равно 3, а в нечетных -4. Всего 7, что соответствует его индивидуальному баллу по всем заданиям.
Коэффициент надежности находим по формуле (3.7.3). В качестве Xi и Yi используются соответственно данные из столбцов «Чет» и «Нечет» соответственно. Вычисления дают для коэффициента надежности следующее значение: rt=0,569.
Поскольку для определения надежности использовалась лишь половина теста, то полученное значение rt является заниженным. Для коррекции значения rt используется формула Спирмена-Брауна
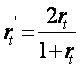 (3.8.5)
(3.8.5)
где rt’ – исправленный коэффициент надежности; rt – коэффициент надежности по половинкам расщепленного теста.
В нашем случае rt’ = 2×0,569/(1+0,569) = 0,725. Исправленное значение показывает удовлетворительную надежность теста (больше +0,7).
Другой способ определения надежности теста основан на использовании среднего коэффициента корреляции всех заданий между собой:
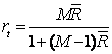 (3.8.6)
(3.8.6)
Здесь M – количество заданий в тесте.
Из таблицы 3.7.2 следует, что
![]()
Тогда
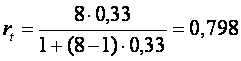
Приведем еще одну формулу, позволяющую рассчитать надежность теста по вариации тестового задания pjqj.
Эта формула носит название KR-20 (F.Kuder & M.Richardson)14 – по имени ее создателей, число 20 – это номер формулы.
 (3.8.7)
(3.8.7)
где M – количество заданий, sX2 – дисперсия индивидуальных баллов испытуемых. Ранее, для дисперсии было получено значение sX2 =4,9.
Расчеты по таблице 3.2.5 дают
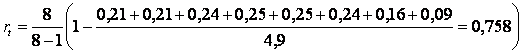
Как видим, вычисления надежности по формулам (3.7.4), (3.7.5), (3.7.6) дают примерно одинаковые результаты.
Выше указывалось, что чем длиннее тест (чем больше в нем заданий) тем он надежнее (при прочих равных условиях). Формула Спирмена-Брауна позволяет оценить требуемую длину теста для заданного значения надежности.
Коэффициент надежности rtk после изменения длины теста равен15
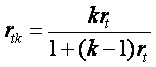 (3.8.7)
(3.8.7)
где k-кратность измерения длины теста; rt – коэффициент надежности до изменения длины теста.
Пусть начальная надежность теста равна 0,758 и количество заданий в тесте увеличивается в два раза. Тогда надежность нового теста равна:
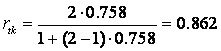
Рассмотрим теперь, обратную задачу. Пусть начальная надежность теста равна 0,758 и мы хотим достигнуть надежности 0.862. Во сколько раз надо увеличить длину теста? Для расчетов воспользуемся формулой
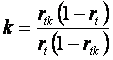
В нашем примере
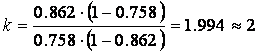
То есть длину теста надо увеличить в два раза.
Рассмотрим теперь вопрос об определении истинного балла испытуемого. Используя регрессионное уравнение11 получим выражение7
![]()
Влияние rt на Ti показано на графиках (рис.3.8.2).
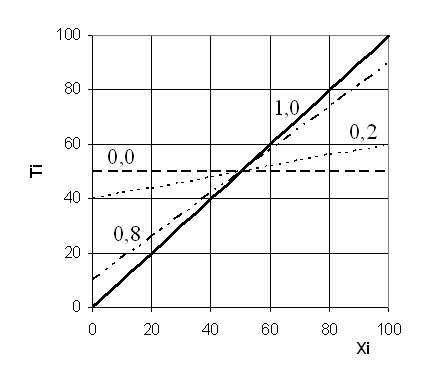
Рис.3.8.2. Влияние надежности теста на истинный балл.
Графики построены в предположении, что средний индивидуальный балл равен 50. Значения коэффициента надежности показаны возле соответствующих зависимостей.
При rt =1 наблюдаемый Xi и истинный Ti баллы совпадают. Этому случаю соответствует прямая линия, проходящая через начало координат под углом 45о к осям. Если надежность теста равна нулю, то определить истинный балл нельзя, для всех испытуемых получается одно и то же значение, равное среднему баллу. Соответственно, график представляет собой горизонтальную прямую, проходящую на уровне 50 баллов. При других значениях rt получаются промежуточные случаи. На рисунке показаны графики для rt =0,2 и rt =0,8. Все зависимости образованы поворотом прямой линии относительно точки закрепления с координатами (50; 50).
Из приведенных графиков видно, что если наблюдаемый балл испытуемого меньше среднего, то Xi < Ti. Если же наблюдаемый балл больше среднего, то Xi > Ti. Иными словами, наблюдаемый балл у слабых испытуемых меньше, а у сильных - больше истинного индивидуального балла.
ОЦЕНКА ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА
Надежность теста определяет ошибку измерения индивидуального балла испытуемого, что позволяет найти стандартную ошибку измерения
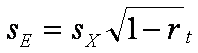
Рассмотрим пример. Ранее, для модельной бинарной матрицы (таблица 3.2.5) нами было вычислено стандартное отклонение SX = 2,214. Коэффициент надежности для этой же матрицы, рассчитанный по формуле Спирмена-Брауна, равен rt= 0, 725. Тогда для стандартной ошибки измерения получим
![]()
Найдем оценку доверительного интервала для доверительной вероятности a = 0,05. Предположим, что середина доверительного интервала совпадает с Xi, а не с Ti. Это, конечно, не так, но мы предположим, что наблюдаемый и истинный тестовый баллы не сильно отличаются. Это вполне справедливо для надежных тестов. Наше допущение приведет к сдвигу границ доверительного интервала, что вызовет ошибку в определении области локализации истинного тестового балла.
Ошибка, допускаемая при этом, получается приемлемой. Тогда половина доверительного интервала равна
δXi = 1,96SE = 1,96×1,161 = 2,27
Теперь найдем границы тестового балла, например, для второго испытуемого X2 = 6 (таблица 3.8.2). Минимальное значение равно 6-2,27=3,73 ≈ 4. Максимальное равно 6+2,27=8,27 ≈ 8. Следовательно, истинный балл испытуемого №2 находится в промежутке от 4 до 8 баллов.
Как видим, вопросу определения надежности теста, необходимо уделять самое пристальное внимание. Созданный на скорую руку «тест» - таковым не является. Это всего лишь совокупность заданий. В лучшем случае, это совокупность заданий в тестовой форме. Только статистическая проверка теста позволяет превратить его в систему тестовых заданий. Только указание его надежности, позволяет адекватно трактовать результаты тестирования.
Таким образом, вопросы определения надежности теста, его стандартной ошибки, области локализации истинного тестового балла очень важны для создания качественного педагогического теста и его дальнейшей сертификации.