Тест, это не просто множество, а система тестовых заданий. Требование системности означает, что между заданиями существуют связи, которые можно обнаружить в результатах тестирования. Определение корреляции, как между заданиями, так и заданий с тестом в целом, позволит оценить системные качества теста. Благодаря такому анализу можно будет выполнить «чистку» - избавить тест от заданий, нарушающих его системные свойства.
Если две величины связаны между собой, то между ними есть корреляция. Виды корреляционной связи показаны в таблице 3.9.
Для выяснения вопроса о наличии связи между двумя величинами X и Y необходимо определить, существует ли соответствие между большими и малыми значениями X и соответствующими значениями Y или такой связи не обнаруживается. Значение каждого элемента Xi и Yi определяется величиной и знаком отклонения от среднего арифметического11:
![]()
Если большие значения Xi соответствуют большим значениям Yi, то это произведение будет большим и положительным, так как
![]() и
и ![]()
То же самое будет наблюдаться и, когда малые значения Xi будут соответствовать малым Yi, поскольку произведение отрицательных чисел будет положительным.
Если же большие значения Xi соответствуют малым значениям Yi, то это произведение будет большим и отрицательным, что будет свидетельствовать об обратной зависимости между этими величинами.
В тех случаях, когда нет систематического соответствия больших значений Xi большим или малым Yi, то знак произведения будет положительным или отрицательным для разных пар Xi и Yi. Тогда сумма
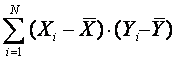
Для того, чтобы эта сумма не зависела от количества значений X и Y, ее следует поделить ее на N-1. Полученная величина sXY называется ковариацией X и Y и является мерой их связи:
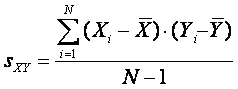
Для исключения влияния стандартных отклонений на величину связи, следует поделить ковариацию sXY на стандартные отклонения sX и sY:
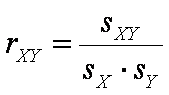
Полученная мера связи между X и Y называется коэффициентом корреляции Пирсона. Обозначение r происходит от слова регрессия. Подставив соответствующие выражения, получим формулу для коэффициента корреляции Пирсона rXY11
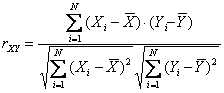
Для вычислений более удобна следующая формула

Коэффициент корреляции Пирсона rXY изменяется в пределах от -1 до +1. В таблице 3.7.1 приведены различные виды линейной зависимости и соответствующие значения rXY.
Следует отметить, что в случае нелинейной связи между X и Y коэффициент корреляции может оказаться близким к нулю, даже если связь очень сильная.
Таблица 3.7.1. Типы корреляционной связи
(Гласс Дж., Стэнли Дж., 1976).

Для решения вопроса о наличии связи между заданиями теста, надо, используя данные по столбцам из бинарной матрицы, рассчитать коэффициенты корреляции Пирсона для каждой пары заданий. Для расчетов используются различные статистические программы (SPSS, STATISTICA и др.). В простейшем случае можно использовать табличный процессор Excel с вызовом функции «ПИРСОН».
В случае дихотомического оценивания (1 - верно, 0 –неверно) выражение для коэффициента корреляции упрощается. Введем следующие обозначения:
pm – доля верных ответов для задания с номером m;
qm – доля неверных ответов для задания с номером m;
pk – доля верных ответов для задания k;
qk – доля неверных ответов для задания с номером k;
pmk – доля верных ответов для задания с номером m и k.
Коэффициент корреляции Пирсона, для дихотомических данных называется коэффициентом «фи». Коэффициент φmk, описывающий связь между заданиями с номерами m и k записывается следующим образом11
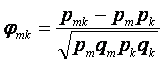
Отметим, что коэффициент «фи» и коэффициент корреляции Пирсона дают в результате одно и то же значение, поскольку обе формулы эквивалентны. Рассмотрим пример вычисления коэффициента корреляции между 2-м и 5-м заданиями. Из таблицы 3.2.5 имеем: p2=0.7, q2=0.3, p5=0.5, q5=0.5. Для определения p25 надо подсчитать количество верных ответов на оба задания одновременно. Видно, что испытуемые с номерами 1-5 успешно справились с обоими заданиями (5 верных ответов). Испытуемые 6 и 7 правильно ответили на 2-е задание, но неправильно на 5-е (нет одновременно верных ответов). Испытуемые 8 и 9 не справились и со 2-м и с 5-м заданиями. Таким образом, p25 =5/10 = 0,5.
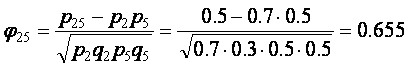
Результаты расчетов для всех заданий приведены в корреляционной матрице (таблица 3.7.2). Корреляционная матрица представляет собой квадратную матрицу размерности MxM, где M – количество заданий, симметричную относительно главной диагонали. В нашем примере матрица имеет 8 строк и столько же столбцов. Коэффициент корреляции Пирсона, скажем, между 2-м и 5-м заданиями находится на пересечении 2-й строки и 5-го столбца (0,655).
В самом последнем столбце располагается коэффициент корреляции каждого задания с тестовым баллом испытуемого (индивидуальным баллом) – rpb – точечный бисериальный коэффициент корреляции.
ТАБЛИЦА 3.7.2. Корреляционная матрица тестовых заданий.
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
rpb |
|---|---|---|---|---|---|---|---|---|---|
|
1 |
1,000 |
0,524 |
-0,089 |
0,218 |
0,655 |
0,089 |
0,327 |
0,218 |
0,634 |
|
2 |
0,524 |
1,000 |
0,356 |
0,218 |
0,655 |
0,089 |
0,327 |
0,218 |
0,738 |
|
3 |
-0,089 |
0,356 |
1,000 |
0,000 |
0,000 |
-0,167 |
-0,102 |
-0,408 |
0,175 |
|
4 |
0,218 |
0,218 |
0,000 |
1,000 |
0,600 |
0,408 |
0,500 |
0,333 |
0,714 |
|
5 |
0,655 |
0,655 |
0,000 |
0,600 |
1,000 |
0,408 |
0,500 |
0,333 |
0,905 |
|
6 |
0,089 |
0,089 |
-0,167 |
0,408 |
0,408 |
1,000 |
0,102 |
0,408 |
0,505 |
|
7 |
0,327 |
0,327 |
-0,102 |
0,500 |
0,500 |
0,102 |
1,000 |
-0,167 |
0,548 |
|
8 |
0,218 |
0,218 |
-0,408 |
0,333 |
0,333 |
0,408 |
-0,167 |
1,000 |
0,365 |
|
|
2,942 |
3,388 |
0,590 |
3,278 |
4,151 |
2,338 |
2,488 |
1,936 |
4,584 |
|
|
0.368 |
0.423 |
0.074 |
0.410 |
0.519 |
0.292 |
0.311 |
0.242 |
0.573 |
Поскольку результаты выполнения тестовых заданий размещаются на дихотомической шкале, а индивидуальный балл испытуемого на интервальной, то формула для коэффициента корреляции Пирсона упрощается и преобразуется в rpb. Выражение для точечного бисериального коэффициента корреляции имеет вид11
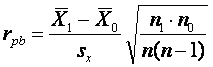
где ![]() - средний индивидуальный балл испытуемых,
справившихся с данным заданием.
- средний индивидуальный балл испытуемых,
справившихся с данным заданием.
![]() - средний
индивидуальный балл испытуемых, не справившихся с данным заданием.
- средний
индивидуальный балл испытуемых, не справившихся с данным заданием.
n1 – число испытуемых, выполнивших данное задание, n0 – число испытуемых, не выполнивших его. n =n1 + n0 – общее количество испытуемых; sx - стандартное отклонение для индивидуальных баллов всех испытуемых.
В нижних строках таблицы 3.7.2 приведены суммарные и среднее значения коэффициента корреляции для каждого задания.
Коэффициент корреляции rpb очень важен, так как характеризует валидность отдельных заданий. Необходимо стремиться к тому, чтобы корреляция результатов по заданию и индивидуальными баллами была достаточно высокой. В.С.Аванесов6 дает следующую рекомендацию: rpb ≥0,5.
Корреляция заданий друг с другом не должна быть слишком высокой (rxy ≤0,3), иначе задания начинают дублировать друг друга6. Если корреляция между двумя заданиями близка к единице, то одно из них лишнее.
Отрицательная корреляция задания с другими заданиями нежелательна. Если задание отрицательно коррелирует с большим количеством других заданий, то это означает, что исход ответов на него противоположен результатам по другим заданиям. По всей вероятности у такого задания либо имеются грубые ошибки в содержании и (или) оформлении (например, нет правильного ответа), либо проверяются знания из другой предметной области.
В нашем примере отрицательной корреляцией отличаются задания 1, 3, 6, 7, 8. Обращает на себя внимание то, что отрицательная корреляция у заданий 1, 6, 7 и 8 наблюдается именно с заданием 3. Это наводит на мысль, что проблематичным является задание 3. В пользу этого свидетельствует и самый низкий средний коэффициент корреляции (0,074) и, самое главное, низкая корреляция с индивидуальными баллами испытуемых (rpb =0.175). Задание 3 следует удалить из теста. В результате отрицательная корреляция останется между 7 и 8 заданиями. Задание 8 находится под подозрением, так как у него rpb =0.365. Это задание также следует удалить из теста. Если какое-либо задание отрицательно коррелирует с индивидуальными баллами (rpb < 0), то такое задание, безусловно, подлежит удалению.