<< Prev | Front | Contents | End | Next >>

4.1. УЧЕТ МОТИВАЦИИ ИСПЫТУЕМЫХ ПРИ ОРГАНИЗАЦИИ ТЕСТОВОГО КОНТРОЛЯ ЗНАНИЙ

При организации учебного процесса весьма важным фактором является учет мотивации к учению. Буквально одно слово преподавателя в определенных условиях может сильно повлиять на учебную мотивацию обучаемого. Согласно Л.И.Божович¹, мотив - это то, ради чего осуществляется  деятельность индивида. Мотивация представляет собой совокупность побуждающих факторов, определяющих активность личности.

Если рассматривать учебный процесс как управляемую систему, то становится очевидной важность такого элемента системы как обратная связь. Именно обратная связь позволяет преподавателю получать информацию о текущем состоянии учебных достижений учащихся, что позволяет выполнять коррекцию хода учебного процесса и эффективно организовывать его. С другой стороны, обратная связь позволяет учащемуся  осуществлять самоконтроль и самодиагностику своего процесса учения.

Обратная связь организуется в разнообразных формах, среди которых все большее применение находят педагогические тесты. Тесты являются объективным инструментом педагогической диагностики, позволяя организовать эффективную систему обратной связи  в современных педагогических технологиях. Следует отметить, что вопросы мотивации в тестировании пока слабо изучены.

Мы предпримем попытку формального учета мотивации испытуемых при анализе результатов тестирования, в частности, при определении поправок на угадывание к тестовому баллу испытуемого.

На практике чаще всего используются тестовые задания с выбором одного или нескольких правильных ответов. Применение таких заданий осложняется попытками испытуемых угадать правильный ответ. Индивидуальный балл испытуемого в этом случае будет отличаться от истинного, что снижает диагностическую ценность тестирования. Вышесказанное обусловливает актуальность проблемы коррекции  результатов тестирования.

В целях упрощения процесса тестирования можно, например, не учитывать вообще вероятность угадывания при обработке результатов тестирования. За правильный ответ испытуемый получает, например,  1 балл, за неправильный - 0 баллов. Поскольку часть баллов получена из-за угадывания, то испытуемые ставятся в неравные условия.  Преимущество получают те, кто отличается  сообразительностью, умеют анализировать задания по формальным и другим признакам, что помогает угадыванию правильного ответа.

Например, в тестовых заданиях  по физике очень часто можно просто проверить размерности итоговых  физических величин в ответах на задание. Если размерности не соответствуют заданию, то эти ответы отбрасываются. При этом уменьшается число ответов, среди которых легче угадать правильный. Иногда это число сокращается до единицы, то есть можно совершенно точно выбрать правильный ответ, даже не читая полностью задания. Существуют и другие способы  анализа ответов, помогающих угадыванию.

Таким образом, игнорирование проблемы угадывания правильных ответов может серьезно снизить доверие к применению заданий с выбором одного правильного ответа, снизить учебную мотивацию.

Рассмотрим различные подходы к решению данной проблемы. В дальнейшем будем предполагать, что каждое задание теста содержит фиксированное количество ответов k, из которых только один правильный.

Хотя задания с выбором одного правильного ответа сильно критикуются за сравнительно высокую вероятность угадывания правильного ответа, эти задания, тем не менее, очень широко распространены. Поэтому анализ именно таких заданий является востребованным на практике. Хотя есть работы, где вместо заданий с выбором одного правильного ответа рекомендуется переходить, где это оправдано, к заданиям с выбором нескольких правильных ответов. В таких заданиях вероятность угадывания резко снижается².

ФИКСИРОВАННАЯ ПОПРАВКА НА КОРРЕКЦИЮ ТЕСТОВОГО БАЛЛА

Допустим, что соблюдается условие равной привлекательности дистракторов в задании.  Кроме того, дистракторы должны быть достаточно привлекательными по сравнению с правильным ответом. Обычно предполагается, что каждый из  дистракторов  должен выбираться не менее чем пятью процентами испытуемых. Тогда  с увеличением количества ответов k в каждом задании вероятность угадывания падает. То есть, поправка должна быть обратно пропорциональна количеству ответов в задании.

В простейшем случае  можно использовать фиксированную поправку, которая определяется следующим образом:

                                        (4.1.1)

Тогда

                   (4.1.2)

где k – количество ответов в задании, Ь – количество заданий в тесте, Y – исправленный индивидуальный балл.

При k = 4  поправка равна 0,25 независимо от значения X.

Соответствующие зависимости показаны на рис.4.1.1.

Из рисунка видно, что исправленная зависимость получается параллельным сдвигом исходного графика на 25 единиц вниз. Индивидуальные баллы испытуемых уменьшаются на величину сдвига исправленного графика. Параллельность графиков означает, что все испытуемые теряют одно и то же количество баллов.

В однопараметрической модели  G.Rasch ( Item Response Theory) поправки  на угадывание не вводятся. Это сделано в трехпараметрической модели:

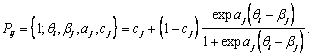
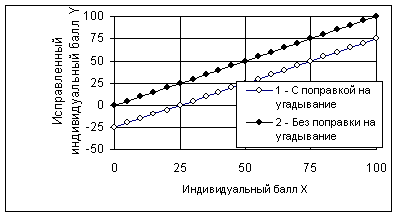
Рис.4.1.1. Исправленный индивидуальный балл с фиксированной поправкой.

Параметр c_j должен  характеризовать вероятность угадывания. За разъяснением смысла остальных величин можно обратиться к работе В.Аванесова³. На рис.4.1.2 приведены соответствующие логистические кривые из работы B.Wright⁴.

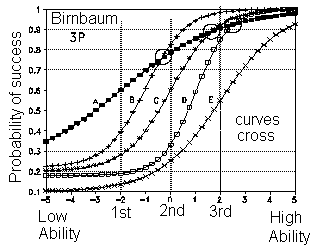
Рис. 4.1.2. Поправка на угадывание в 3-х параметрической модели  IRT (B.Wright, 1992).

Из рисунка видно, что учет поправки на угадывание приводит к смещению кривых вверх по оси ординат.

Введение постоянных поправок лишь частично решает проблему и педагогически мало оправданно, так как в этом случае не различаются сильные и слабые испытуемые. В этом методе априори считается, что и сильный и слабый испытуемые в одинаковой степени пытаются угадать правильный ответ. Разумеется, это неверно. Сильный испытуемый не нуждается в угадывании, его знаний достаточно, чтобы с высокой вероятностью успешно справиться с заданием.

Таким образом, фиксированные поправки вводятся достаточно просто, но с педагогической точки зрения они могут быть не эффективны, поскольку не учитывают мотивацию сильных и слабых испытуемых. Для того чтобы учесть различие в мотивации к угадыванию у сильных и слабых испытуемых необходимо использовать поправку Δp₁, зависящую от  доли правильных ответов

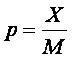
или от доли неправильных ответов  q = 1 – p.

Итак, задача состоит в том, чтобы попытаться предугадать поведение испытуемого и внести коррекцию в его индивидуальный балл.

Представляется разумным считать, что чем ниже уровень знаний испытуемого, тем сильнее его стремление восполнить недостаток знаний простым угадыванием правильного ответа, без применения тех или иных методик выбора правильного ответа по формальным признакам. Если же испытуемый хорошо подготовлен, то есть обладает малым значением q = 1 – p, то его стремление к угадыванию будет очень слабым и поправка должна быть малой.

Иными словами, чем больше q, тем больше должна быть поправка. С другой стороны, чем больше k – количество ответов в задании, тем меньше должна быть поправка. 

Обозначим через Y – исправленный индивидуальный балл испытуемого. Эту величину можно вычислить по формуле:

где ΔX – поправка к индивидуальному баллу испытуемого.

Используем соотношения X=p·M     и   ΔX=Δp·M,

где  Δp - поправка к доле правильных ответов испытуемого.

С учетом этих соотношений, исправленный индивидуальный балл перепишем в виде:

Y = ( p +Δp)·M

Примем, что поправка Δp₁  прямо пропорциональна q:

В этом случае исправленный индивидуальный балл равен

                      (4.1.3)

Соответствующая зависимость показана на рис. 4.1.3.

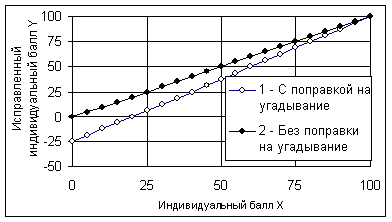
Рис. 4.1.3. Индивидуальный балл, исправленный с использованием Δp₁.

Из рис. 4.1.3 наглядно видно, что для сильных испытуемых с высокими значениями индивидуального балла поправки имеют малое значение и стремятся к нулю при X стремящемуся к M. Ситуация заметно улучшилась, по сравнению с тем, что показано на рис. 4.1.1. Отметим, что формула (4.1.3) почти  не получила практического применения из-за своей слабой педагогической и психологической обоснованности. Отметим, что при  X = 25 (четвертая часть всех заданий), в рассматриваемом приближении логично предположить, что поправка  равна индивидуальному баллу (ΔX = 25). Тогда исправленный балл должен быть равен нулю (Y = 0). Однако, из рис.4.1.3 следует, что Y = 6,25 балла.

Таким образом, требуется дать большее обоснование действию механизма поправки и желательно не ограничиваться линейными приближениями.

Предположим, что поправка  Δp   нелинейно зависит от доли неправильных ответов следующим образом:

                          Δp =μ·qⁿ,                             (4.1.4)

где n  - натуральное число,    m - некоторый коэффициент, подлежащий определению.

Для определения   μ  примем во внимание два следующих обстоятельства.

Во-первых, в большинстве тестовых заданий, используемых на практике значение k находится в пределах  3 … 5.

Во-вторых, при малых значениях индивидуального балла испытуемого разумно предположить, что низкий уровень знаний  способствует стремлению угадывать правильный ответ.

Что же считать низким уровнем знаний? Практически это следующие значения  доли верных ответов

p₀ = 0,2 … 0,3.

Из этих двух обстоятельств следует предположение, что

Иными словами, можно считать, что индивидуальный балл испытуемого полностью угадан и исправленный индивидуальный балл должен быть равен нулю, то есть

p₀ = Δp_const  = μ·qⁿ.

Таким образом, получаем

или

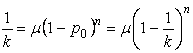
отсюда имеем

Таким образом, коэффициент  μ  равен

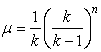                      (4.1.5)

Зная коэффициент    m,  мы можем записать выражение для исправленного индивидуального балла испытуемого.

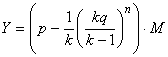     (4.1.6)

Мы получили формулу, позволяющую вводить поправки на угадывание, используя различные нелинейные  модели.

Ввиду важности обоснования этой формулы еще раз приведем оба положения, лежащие в основе рассуждений:

1) в практическом тестировании используются  тестовые задания с k =3…5;

2) значения p₀ = 0,3 … 0,2 считаются низкими и полностью обусловленными угадыванием. Исходя из этого,  мы можем приближенно считать, что p₀ = 1/k.

Используя выражение (4.1.6) для исправленного индивидуального балла испытуемого, рассмотрим различные модели коррекции и проведем их сравнительных анализ.

ФИКСИРОВАННАЯ ПОПРАВКА, n=0

Подставив n=0 в формулу (4.1.6), получим тестовый балл с фиксированной поправкой (см.формулу (4.1.2))

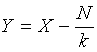
Как указывалось выше, фиксированные поправки не учитывают мотивацию испытуемых и малопригодны в педагогическом тестировании.

ЛИНЕЙНАЯ МОДЕЛЬ, n = 1

В этом случае из формулы (4.1.6) имеем:

               (4.1.7)

Поскольку X = pM  и  W = qM, то можно переписать это выражение в другом виде

                                  (4.1.8)

где W - количество неверных ответов испытуемого.

Эта формула   хорошо известна и давно используется в практике тестирования. Линейная модель широко применяется  и формула (4.1.8) приведена, например, в работе В.С.Аванесова⁵. 

В таблице 4.1.1 приведены значения исправленного индивидуального балла в линейной модели, а на рис.4.1.4 - соответствующие зависимости.

Из таблицы 4.1.1 видно, что с ростом индивидуального балла испытуемого, его поправка на угадывание стремится к нулю. В этой модели предполагается, что при 25% правильных ответов, исправленный индивидуальный балл равен нулю (Y=0), то есть объем знаний испытуемого равен нулю и все правильные ответы получены путем угадывания.

Таблица 4.1.1. Поправка на угадывание в линейном приближении, при k = 4.

X, индивидуальный балл	ΔX, поправка	Y, исправленный индивидуальный балл
0	-33	-33
25	0	0
50	17	33
75	8	67
100	0	100

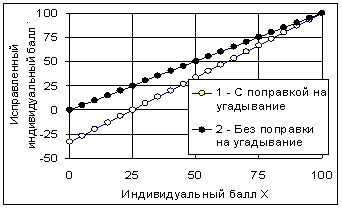
Рис.4.1.4.  Коррекция индивидуального балла в линейной модели.

Если индивидуальный балл равен 100, то поправка отсутствует и исправленный индивидуальный балл совпадает с исходным, то есть тоже равен 100. В этом случае предполагается, что испытуемый не имел стимула отвечать наугад, так как располагал достаточно полным объемом знаний.

При низких индивидуальных баллах (X < 25) получаются отрицательные поправки, что не имеет смысла. Поэтому в этих случаях следует просто считать, что исправленный индивидуальный балл просто равен нулю (Y=0).

Отметим, что для X = 25 следует Y = 0, что соответствует логике наших рассуждений.

НЕЛИНЕЙНАЯ, ПАРАБОЛИЧЕСКАЯ МОДЕЛЬ, n = 2

Подставив n = 2 в формулу (4.1.6), получим для параболической модели выражение для  исправленного индивидуального балла:

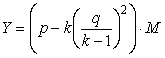                  (4.1.9)

Таблица 4.1.2. Поправка на угадывание в параболическом приближении, при k = 4.

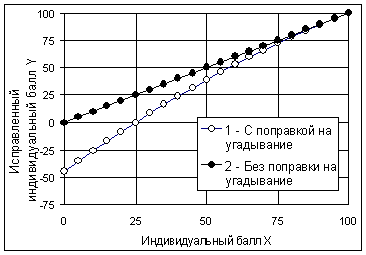
Рис. 4.1.5.  Коррекция индивидуального балла в параболической модели.

В этой модели, как и предыдущем случае для X = 25 следует Y = 0. Из таблицы 4.1.2 следует, что наблюдается более жесткая реакция на угадывание для слабых испытуемых. Для  сильных же испытуемых коррекция меньше, чем в линейной модели (4.1.7). Соответствующие графические зависимости приведены на рис. 4.1.5.

НЕЛИНЕЙНАЯ, КУБИЧЕСКАЯ МОДЕЛЬ, n = 3

Подставив n = 3 в формулу (4.1.6), получим для параболической модели выражение для  исправленного индивидуального балла:

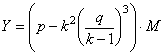                          (4.1.10)

Результаты расчетов приведены в таблице 4.1.3 и на рис. 4.1.6.

Таблица 4.1.3. Поправка на угадывание в кубическом приближении, при k = 4.

В кубической модели наблюдается усиление тенденции, проявившейся в параболической модели. К слабым испытуемым предъявляются еще более жесткие требования, а к сильным - значительно более мягкие.

Рассмотрение поправок для n > 3 нами не проводится, так как тенденция ясна и практического значения сильно нелинейные модели почти не  имеют.

В психологическом плане, возрастание показателя n можно трактовать усиление недоверия к слабым испытуемым и наоборот, усиление доверия к сильным испытуемым.

Сфера применения тех или иных моделей определяется педагогическими условиями, в которых проводится тестирование. Возможны ситуации, когда можно обойтись вообще без коррекции тестового балла. Чаще всего коррекция все-таки нужна, что обусловлено педагогической целесообразностью, стремлением повысить валидность тестовых результатов. 

Нелинейные модели можно рекомендовать к применению в группах испытуемых с четко выраженным разделением на сильных и слабых.

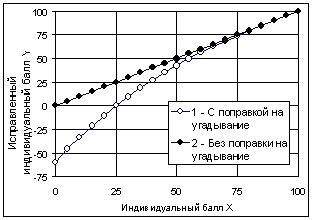
Рис.4.1.6.  Коррекция индивидуального балла в кубической модели.

Таким образом, для правильной организации процесса тестирования необходимо вводить поправки на угадывание. При этом необходимо учитывать различие в мотивации к угадыванию у различных групп испытуемых.

<< Prev | Front | Contents | End | Next >>