
При разработке тестовых заданий важно оценить их качество, что делается в рамках той или иной модели. В данном параграфе продолжен21, 22 анализ тестовых заданий, выполняемый на основе теории G.Rasch. Для анализа данных использовались задания по учебной дисциплине «Базы данных» (Федеральный компонент, ОПД.Ф.03) и программное средство RUMM (Rasch Unidimensional Measurement Model), разработанное под руководством профессора D.Andrich23. Программное средство RUMM успешно используется для оценки качества тестовых заданий во многих странах мира.
Для однопараметрической модели измерения (1PL) вероятность успеха i-го испытуемого в j-м задании равна

где d – коэффициент шкалирования, равный 1,702.
θi (ability) - степень подготовленности испытуемого
Исходный набор заданий содержал 72 задания с выбором одного правильного ответа из четырёх, предлагавшихся на выбор. Всего было протестировано 40 испытуемых.
Все испытуемые были распределены по шкале θ по своим диапазонам уровня подготовленности. Испытуемые были поделены на K групп (классов интервалов) вдоль шкалы θ так, чтобы все тестируемые внутри данной группы имели одинаковый уровень подготовленности θk. Всего внутри группы с номером k окажутся mk тестируемых, где k принимает значения из интервала k = 1,2,3,…,K.
В RUMM-2020 значение K по умолчанию устанавливается равным 3, но при необходимости его можно изменить, используя параметр «Class_Intervals» в диалоговом окне «Analysis Control». Чем большим берётся число классов, тем больше «эмпирических» точек представляется на графике заданий. Однако в этом случае требуется иметь и большее число испытуемых. Вот почему при небольшом числе испытуемых минимально допустимым принимается число классов, равное трём, так как по двум точкам на теоретической кривой ICC трудно судить о соответствии задания модели Раша.
В настоящем исследовании в первый классовый интервал данных были включены 13 испытуемых, во второй - 12 и в третий - 15 испытуемых. Точки, соответствующие этим интервалам, имеют значения q, равные соответственно 0.636, 2.751 и 3.638.
Далее в работе приведены рисунки с изображениями характеристических кривых некоторых заданий - Item Characteristics Curves (ICC). Для каждой группы приведены примеры ICC для двух заданий. На рис.5.8.1 приведены примеры ICC, иллюстрирующие смысл некоторых параметров, характеризующих ICC. На рис.5.8.2-5.8.9 приведены ICC для заданий анализируемого теста.
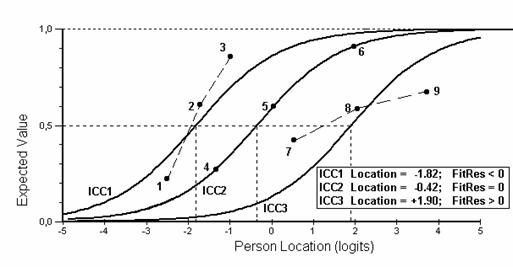
Рис. 5.8.1. Пример характеристических кривых трех заданий.
Для оценки степени соответствия данных модели Раша в RUMM2020 используется распределение хи-квадрат (χ2probability). Чем ближе значения этого распределения к единице, тем лучше соответствие данных модели. соответственно, чем ближе к нулю, тем хуже соответствие задания модели измерения по теории Раша.
Для каждой кривой приведены следующие параметры, которые рассмотрим на примере ICC-53 (рис. 5.8.2). Описание основных свойств параметров приведено в работе А.Маслака4. Ниже следует это описание с нашими дополнениями.
I0053 - код (идентификатор) тестового задания;
Descriptor for item 53 - заголовок (название) тестового задания 53. Вообще-то при редактировании вводимых данных в RUMM можно использовать в качестве названия произвольный текст. В данном случае выбрано значение по умолчанию;
Locn = 0,902 - трудность тестового задания в логитах.
На рис. 5.8.1 в качестве примера показаны три характеристические кривые ICC1, ICC2, ICC3 для некоторых заданий со значениями Locn (Location) равными -1.82, -0.42, +1.90. Для каждой кривой Locn – это значение Person location, при котором вероятность правильного ответа на данное задание равно 0.5.
FitRes = -0,358 - суммарное отклонение ответов испытуемых на данное задание от ожидаемых на основе модели Раша. Если параметр FitRes = 0, то мы имеем совпадение ответов испытуемых с моделью Раша. Большие по абсолютной величине значения FitRes свидетельствуют о расхождении экспериментальных данных с моделью Раша. Схематически это показано на рис. 5.8.1, где в качестве примера показаны характеристические кривые, имеющие различные значения параметра FitRes.
Для характеристической кривой ICC1 экспериментальным точкам 1,2 и 3 соответствует отрицательное значение параметра FitRes. Здесь мы имеем дело со сверхдифференцирующей способностью тестового задания. Эти экспериментальные данные плохо соответствуют модели Раша. Необходимо дополнительно проверить значение параметра χ2probability. Если оно менее чем 0.05, то задание следует исключить из теста.
Для кривой ICC2 (точки 4, 5 и 6) параметр FitRes=0, что свидетельствует о соответствии экспериментальных данных модели Раша.
Для кривой ICC3 (точки 7, 8 и 9) параметр FitRes > 0, что свидетельствует о плохом соответствии модели Раша. Это тестовое задание со слабой дифференцирующей способностью. Для решения вопроса об исключении задания из теста необходимо, как и в случае ICC1, проверить значение χ2probability.
ChiSq[Pr] = 0,872 - мера соответствия данных модели Раша на основе проверки эмпирического и теоретического значений распределения хи-квадрат (χ2probability). Если ChiSq[Pr] меньше критического значения 0.05, то задание следует исключить из теста;
Slope = 0,25 – наклон ICC в точке перегиба (θj = βj). Этот параметр характеризует теоретическую дифференцирующую способность задания – способность тестового задания различать испытуемых по уровню их знаний. В дихотомическом случае наклон всех ICC одинаков, что хорошо видно на рис. 5.8.1.
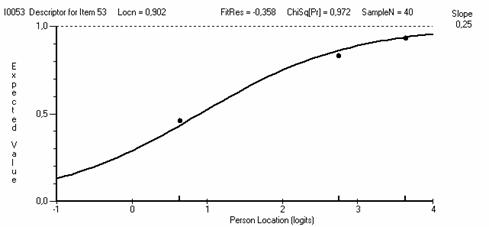
Рис. 5.8.2. ICC для задания №53 с c2prob = 0.972, входящего в состав первой группы.
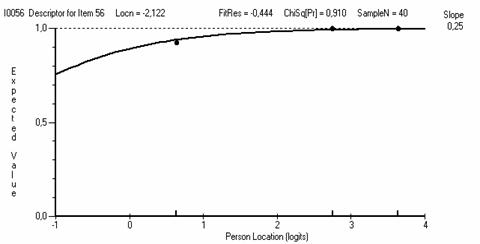
Рис. 5.8.3. ICC для задания №56 с c2prob = 0.910, входящего в состав первой группы.
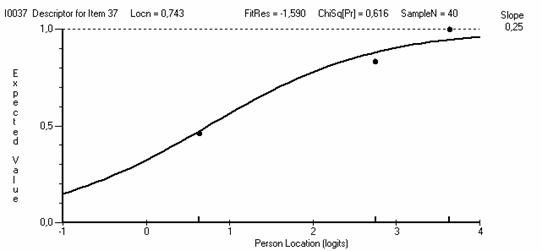
Рис. 5.8.4. ICC для задания №37, c2prob = 0.616, входящего в состав второй группы.
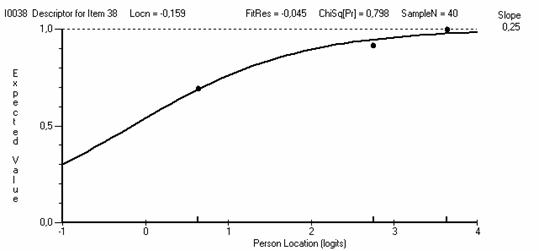
Рис. 5.8.5. ICC для задания №38 с c2prob = 0.798, входящего в состав второй группы.
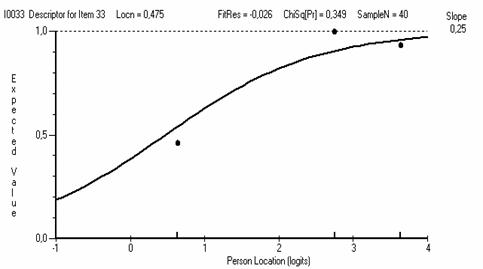
Рис. 5.8.6. ICC для задания №33 с c2prob = 0.349, входящего в состав третьей группы.
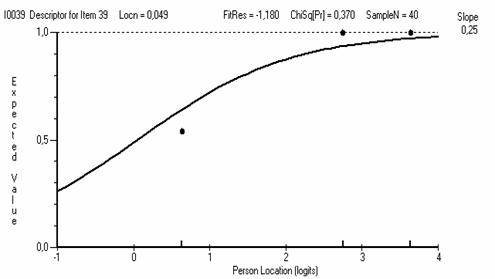
Рис. 5.8.7. ICC для задания №39 с c2prob = 0.370, входящего в состав третьей группы.
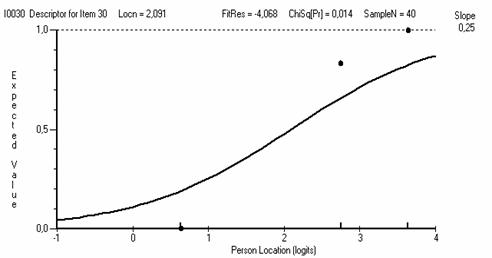
Рис. 5.8.8. ICC для задания №30 с c2prob = 0.014, входящего в состав четвертой группы.
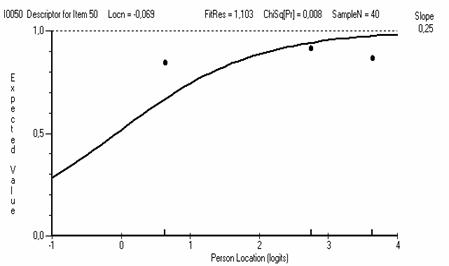
Рис. 5.8.9. ICC для задания №50 с c2prob = 0.008, входящего в состав четвертой группы.
Как отмечалось выше, параметр χ2probability позволяет судить о степени соответствия экспериментальных данных модели Раша. По величине χ2probability все экспериментальные данные были распределены по четырем группам:
| группа №1 χ2probability ≥ 0.8, | 11 заданий; |
|
группа №2 0.6 ≤ χ2probability < 0.8, |
13 заданий; |
|
группа №3 0.05 ≥ χ2probability < 0.6, |
39 задания; |
| группа №4 χ2probability < 0.05, | 9 заданий. |
В таблице 5.8.1 приведено распределение тестовых заданий по всем четырем группам. В ней данные представлены следующим образом. Допустим, нас интересует - в какую группу попадает задание №45? На пересечении столбца «40» и строки «5» находится число «1» - первая группа, следовательно, 45-е задание имеет χ2probability ≥ 0,8.
Таблица 5.8.1. Распределение тестовых заданий по группам χ2probability.
|
No Задания |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
|
0 |
- |
3 |
2 |
4 |
4 |
4 |
2 |
2 |
|
1 |
3 |
3 |
1 |
3 |
3 |
3 |
3 |
3 |
|
2 |
3 |
1 |
3 |
3 |
3 |
3 |
3 |
3 |
|
3 |
1 |
3 |
3 |
3 |
4 |
1 |
3 |
- |
|
4 |
2 |
3 |
3 |
3 |
2 |
3 |
3 |
- |
|
5 |
3 |
2 |
4 |
2 |
1 |
1 |
3 |
- |
|
6 |
3 |
3 |
2 |
3 |
2 |
1 |
3 |
- |
|
7 |
3 |
4 |
1 |
2 |
4 |
1 |
4 |
- |
|
8 |
4 |
3 |
1 |
2 |
3 |
3 |
3 |
- |
|
9 |
1 |
3 |
2 |
3 |
2 |
3 |
3 |
- |
Каждое задание характеризуется своей мерой трудности. Этот параметр можно охарактеризовать проекцией точки перегиба логистической кривой на ось θ. Для определения трудности задания следует на графике провести горизонтальную прямую с ординатой P=0.5 до пересечения с характеристической кривой (ICC), затем опустить перпендикуляр на ось θ. Отметим, что в RUMM сразу проводится вычисление этого значения θ (Location), которое показано на графиках ICC.
В таблице 5.8.2 приведено распределение заданий по степени трудности. В таблице строка «id» обозначает номер задания, а строка «Lcn» - обозначает значение θ, для которого вероятность правильного ответа равна P=0,5.
Из таблицы 5.8.2 видно, что задания теста с удовлетворительной равномерностью покрывают диапазон θ от -2,4 до +2,1 логитов.
Обычно считается, что тест должен перекрывать диапазон от -3 до +3 логитов. Это означает, что в анализируемом тесте не хватает очень легких и очень трудных заданий. В существующем виде тест больше предназначен для испытуемых со средними способностями.
Таблица 5.8.2. Распределение заданий по уровню их трудности.
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
id |
27 |
12 |
28 |
56 |
24 |
67 |
57 |
45 |
21 |
11 |
|
Lcn |
-2,365 |
-2,324 |
-2,122 |
-2,122 |
-1,687 |
-1,645 |
-1,414 |
-1,405 |
-1,388 |
-1,303 |
|
№ |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
id |
69 |
25 |
5 |
17 |
60 |
70 |
49 |
59 |
58 |
48 |
|
Lcn |
-1,303 |
-1,192 |
-1,183 |
-1,176 |
-0,953 |
-0,909 |
-0,871 |
-0,815 |
-0,796 |
-0,672 |
|
№ |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
|
id |
18 |
32 |
20 |
4 |
65 |
46 |
36 |
26 |
72 |
23 |
|
Lcn |
-0,589 |
-0,579 |
-0,563 |
-0,5 |
-0,494 |
-0,472 |
-0,455 |
-0,452 |
-0,379 |
-0,273 |
|
№ |
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
|
id |
40 |
38 |
50 |
19 |
64 |
39 |
35 |
54 |
66 |
29 |
|
Lcn |
-0,272 |
-0,159 |
-0,069 |
-0,008 |
0,03 |
0,049 |
0,055 |
0,117 |
0,215 |
0,257 |
|
№ |
41 |
42 |
43 |
44 |
45 |
46 |
47 |
48 |
49 |
50 |
|
id |
14 |
31 |
41 |
71 |
33 |
55 |
47 |
13 |
16 |
22 |
|
Lcn |
0,27 |
0,305 |
0,31 |
0,447 |
0,475 |
0,484 |
0,496 |
0,5 |
0,5 |
0,687 |
|
№ |
51 |
52 |
53 |
54 |
55 |
56 |
57 |
58 |
59 |
60 |
|
id |
9 |
10 |
3 |
43 |
37 |
53 |
6 |
2 |
68 |
61 |
|
Lcn |
0,693 |
0,728 |
0,731 |
0,742 |
0,743 |
0,902 |
1,016 |
1,025 |
1,103 |
1,104 |
|
№ |
61 |
62 |
63 |
64 |
65 |
66 |
67 |
68 |
69 |
70 |
|
id |
52 |
42 |
7 |
62 |
44 |
1 |
51 |
15 |
63 |
34 |
|
Lcn |
1,208 |
1,259 |
1,264 |
1,285 |
1,364 |
1,416 |
1,42 |
1,594 |
1,855 |
1,955 |
|
№ |
71 |
72 |
73 |
74 |
75 |
76 |
77 |
78 |
79 |
80 |
|
id |
30 |
8 |
- |
- |
- |
- |
- |
- |
- |
- |
|
Lcn |
2,091 |
2,21 |
- |
- |
- |
- |
- |
- |
- |
- |
Перейдем к обсуждению качества тестовых заданий на основании полученных характеристических кривых (рис. 5.8.2-5.8.9).
Из графиков видно, что экспериментальные данные для всех заданий расположены в области от 0 до 4 логитов.
Задания, входящие в первую группу (например, с ICC, показанными на рис. 5.8.2 и 5.8.3) имеют отличное согласие с моделью Раша и оставляются в тесте.
Задания, входящие во вторую группу (например, с ICC, показанными на рис. 5.8.4 и 5.8.5) имеют хорошее согласие с моделью Раша и также оставляются в тесте.
Задания, входящие в третью группу (например, с ICC, показанными на рис. 5.8.6 и 5.8.7) имеют удовлетворительное согласие с моделью Раша. Такие задания можно оставить в тесте. Отметим, что эти задания желательно дополнительно проанализировать с точки зрения их содержания. Желательно собрать дополнительную статистику на предмет выявления отклонений в процедуре тестирования.
Задания, входящие в четвертую группу (например, с ICC, показанными на рис. 5.8.8 и 5.8.9) не согласуются с моделью Раша. Такие задания следует исключить из теста.
Из рис. 5.8.6 видно, что задание №33, характеризующееся значением χ2probability = 0.349, имеет удовлетворительное согласие с моделью Раша, но имеет аномальный участок - сильные испытуемые отвечают хуже, чем испытуемые со средним уровнем знаний. В.Аванесов связывает подобные эффекты с нарушениями формальных, организационных и этических требований. В связи с тем, что аномальный эффект проявляется лишь частично, а χ2probability > 0.05, то это задание можно временно оставить в изучаемом наборе заданий, имея в виду дальнейшую проверку теста в целом.
На рис.5.8.8 приведена логистическая кривая для задания №30 с χ2probability = 0.014. Это задание имеет сверхвысокую дифференцирующую способность, то есть имеет малый диапазон перекрытия по уровню знаний испытуемых. Экспериментальные данные показывают, что слабые испытуемые практически не могут дать верный ответ на это задание. С другой стороны, средние и сильные испытуемые на это задание отвечают гораздо лучше, чем того требует модель Раша. Как указывалось выше, ввиду несоответствия модели Раша, подобные задания исключаются из теста.
Пример логистической кривой для задания №50 (χ2probability = 0.008) с практически полным отсутствием дифференцирующей способности приведен на рис. 5.8.9. Это задание почти не различает слабых, средних и сильных испытуемых.
Это довольно легкое задание (Location = -0,069), но сильные испытуемые показывают такую же вероятность успеха, как средние и слабые, что противоречит модели Раша. Кроме того, это задание плохо соответствует другим заданиям и по всем этим причинам должно быть удалено из теста.
Таким образом, анализ результатов тестирования на основе подхода Rasch measurement позволяет оптимизировать содержание теста и превращать его в инструмент для измерения уровня знаний испытуемых. Особенно удобно это делать с применением программного средства RUMM