Ким В.С., Тестирование учебных достижений. - Уссурийск, 2007
1.6. ИЗМЕРИТЕЛЬНЫЕ ШКАЛЫ
Поскольку мы рассматриваем тест как средство
педагогического измерения, то, как и во всех измерениях, нам следует сначала
рассмотреть вопрос об измерительных шкалах. В измерениях используется много
различных шкал, мы рассмотрим четыре основные шкалы69, 70, 71, 72.
Согласно Пфанцаглю И.69, шкала задается группой допустимых
преобразований. Номинальная шкала (шкала наименований) задается группой всех
взаимнооднозначных преобразований, шкала порядка - группой всех строго
возрастающих преобразований.
ШКАЛА НАИМЕНОВАНИЙ используется для идентификации элементов
множества. На этой шкале определены две операции - «равно» и «не равно».
Номинальная шкала допускает те преобразования, которые, у одинаковых объектов
оставляет одинаковые имена (идентификаторы). Это могут быть имена собственные,
названия городов и т.д. Рассмотрим пример трех множеств из пяти элементов.
Первое множество образуют фамилии людей, второе - знаки зодиака, третье -
номера комнат. Элементы этих множеств приведены в таблице.
Элементы номинальной шкалы.
|
№
|
Множество 1
«фамилии»
|
Множество - 2
«знаки зодиака»
|
Множество - 3
«номера комнат»
|
|
1
|
Иванов
|

|
27
|
|
2
|
Сидоров
|
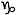
|
81
|
|
3
|
Петров
|
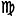
|
108
|
|
4
|
Алексеев
|
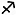
|
312
|
|
5
|
Яковлев
|
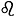
|
105
|
Значения на номинальной шкале всего лишь дают возможность отличить один
объект от другого. Эти значения не могут быть упорядочены и рассматриваются
изолированно друг от друга.
Специально отметим, что числа, приведенные в последнем столбце
(Множество - 3), числами не являются. Это «имена» комнат. С ними нельзя,
например, выполнить действие сложения: 27+81=108. Тем более, на номинальной
шкале нельзя выполнять арифметические операции умножения и деления.
ШКАЛА ПОРЯДКА, как и шкала
наименований, является качественной, но позволяет не только именовать, но и ранжировать элементы множества.
Порядковая шкала допускает только монотонные преобразования, то есть такие,
которые не нарушают порядок следования значений измеряемых величин. Самый яркий
пример порядковой шкалы - это шкала Мооса для твердости минералов.
|
Минерал
|
Твердость
по Моосу
|
|
Тальк
|
1
|
|
Гипс
|
2
|
|
Кальцит
|
3
|
|
Флюорит
|
4
|
|
Апатит
|
5
|
|
Ортоклаз
|
6
|
|
Кварц
|
7
|
|
Топаз
|
8
|
|
Корунд
|
9
|
|
Алмаз
|
10
|
При построении шкалы твердости рассуждали следующим образом: тальк -
самый мягкий минерал, им ничего нельзя поцарапать, поэтому ему присвоена самая
низкая твердость. Гипс царапает тальк, следовательно, он тверже и ему
присваивается твердость, равная двум. В свою очередь, кальцит царапает гипс,
значит, он еще тверже и ему приписывается твердость 3. Самым твердым
оказывается алмаз, который царапает все минералы и ни один минерал не царапает
его.
Отличительной особенностью порядковой шкалы является то, что значения по
этой шкале упорядочены. В рассмотренном примере минералы строго упорядочены по
своей твердости. Пусть мы хотим определить твердость неизвестного минерала.
Проведем серию испытаний, пытаясь поцарапать известные минералы. Допустим,
оказалось, что мы можем поцарапать кварц, но не можем корунд. Значит наш
минерал тверже кварца, но мягче корунда. Следовательно, твердость нашего
минерала равна 8. Отметим, что мы не знаем насколько
наш минерал тверже кварца, такую информацию порядковая шкала не содержит.
Другой пример - это школьные отметки.
|
Уровень знаний
|
Отметка
|
|
Совершенно
неудовлетворительно
|
1
|
|
Неудовлетворительно
|
2
|
|
Удовлетворительно
|
3
|
|
Хорошо
|
4
|
|
Отлично
|
5
|
Отметки имеют свои имена (1, 2, 3, 4, 5) и упорядочены. Нам известно,
что 4 означает более высокий уровень знаний, чем 3, но не известно насколько. С
отметками нельзя выполнять арифметические операции: 5-4=1, 3-2=1, 5-4=3-2 и т.д.. Ясно, что различие в знаниях между
отличником и хорошистом не такое же, как между троечником и двоечником. Это
общеизвестный факт. С другой стороны в образовательных учреждениях широко
практикуется средний балл. Для определения среднего балла складывают,
например, все отметки за год и делят на
их количество. Это недопустимо. Ни
складывать, ни делить отметки нельзя, так как они расположены на порядковой
шкале*.
ШКАЛА ИНТЕРВАЛОВ, в отличие от шкалы порядка,
позволяет не только
ранжировать элементы множества, но и задает известные интервалы между
элементами. Интервальная шкала допускает линейные преобразования вида:
y = a · x + b
где а - положительное
число, b - положительное
или отрицательное число.
Изменение a приводит к изменению масштаба шкалы, изменение b вызывает сдвиг по шкале, то есть положение нуля на интервальной шкале не определено. Интервальные шкалы используются, например,
для измерения температуры. При этом температурные интервалы равны, а положение
нуля зависит от вида температурной шкалы, например по Цельсию, или по Фаренгейту. Если это
неизвестно, то для описания закономерностей следует использовать отношение
интервалов:
| y1 - y2 |
= |
(ax1 + b) - (ax2 + b) |
| y3 - y4 |
(ax3 + b) - (ax4 + b) |
ШКАЛА ОТНОШЕНИЙ допускает линейные
преобразования вида:
y = a · x
Шкала отношений, в
отличие от интервальной шкалы, обладает точкой нулевого отсчета. Этот тип шкал
используется для измерения массы тела, его длины и так далее. Например, длина
может измеряться в метрах, футах, парсеках - это определяется масштабным
множителем a. Если нам неизвестны единицы измерения, то для описания закономерностей
следует использовать отношение
величин, которое является инвариантом для шкалы отношений.
* Говорят, Лев Ландау ввел 10-ти бальную шкалу для оценивания женской красоты. Если это так, то его шкала должна быть порядковой.
Ким В.С., Тестирование учебных достижений. - Уссурийск, 2007