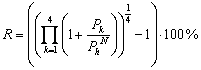
Одним из доводов против заданий с выбором одного верного ответа является утверждение, что испытуемые могут запомнить неверные ответы (дистракторы) и это приведет к снижению их уровня подготовленности. В заданиях с выбором наилучшего ответа можно дать все ответы верные, но в различной степени. Метод оценивания всех ответов (grading) сильно усложняет задачу испытуемого. Назовем такие задания - заданиями с градуированными ответами. В литературе эти задания имеют разные названия – «задания с выбором наилучшего ответа»2, «задания с множественным выбором»11. В таких заданиях испытуемому надо не просто выбрать верный ответ, но еще дать свою оценку остальным ответам. Угадывание в такой ситуации практически исключено. Отметим, что в вариантах ответов иногда указывают и неверные ответы.
Пример № 30.
ЕСЛИ ЗА РАВНЫЕ ПРОМЕЖУТКИ ВРЕМЕНИ ТЕЛО ПРОХОДИТ РАВНЫЕ РАССТОЯНИЯ, ТО ЭТО ДВИЖЕНИЕ
1) равномерное
2) с постоянной скоростью
3) без ускорения
4) неравномерное
Разработчик задания предположил, что первому ответу, как наиболее правильному, соответствует оценка «5», второму, менее правильному» - «4», третьему – «3» и четвертому, неправильному – «2». Такие градуированные задания, (задания с множественным оцениванием), порождают ряд проблем.
Во-первых, крайне сложно создать градуированные ответы однозначно, оцениваемые разными людьми, что обусловлено их субъективизмом.
Во-вторых, достаточно сложная процедура оценивания задания в целом.
Рассмотрим эти проблемы. Нередки случаи, когда за один и тот же ответ учащегося два разных учителя ставят разные оценки. К.Ингенкамп15 указывает, что расхождение может составлять 2 балла (от 3 до 5). Мало того, один и тот же учитель за один и тот же ответ (видеозапись, показанная с интервалом несколько месяцев) ставит разные оценки. Рассмотрим вышеприведенное задание (Пример № 30.. Разработчик задания оценивает второй ответ на «4», а другой эксперт вполне может счесть, что этот ответ заслуживает оценки «5». Относительно легко градуированные задания создаются с использованием принципа кумуляции.
Пример № 31.
СИЛА ПЕРЕМЕННОГО ТОКА НА УЧАСТКЕ ЦЕПИ ОПРЕДЕЛЯЕТСЯ
1) емкостью
2) емкостью и индуктивностью
3) емкостью, индуктивностью и активным сопротивлением
4) емкостью, индуктивностью, активным сопротивлением и реактивным
сопротивлением
Целью задания было выяснить – знает ли испытуемый, что сопротивление переменному току оказывают емкость (конденсатор), индуктивность (катушка индуктивности) и активное сопротивление (резистор). В этом задании использован принцип кумуляции, что позволяет произвести точное оценивание ответов. 3-й ответ самый полный (указаны три параметра) – оценка «5». Второй ответ менее полный (два параметра) – оценка «4», Первый ответ верный, но неполный (1 параметр) - оценка «3». Четвертый ответ – неверный – оценка «2». Логика оценивания была такая. Выбор четвертого ответа означает, что испытуемый неплохо знает, какие параметры влияют на силу переменного тока, но не понимает, что емкость и индуктивность как раз - таки задают реактивное сопротивление. Указание реактивного сопротивления сводит на нет, положительный эффект от указания емкости и индуктивности. Поэтому оценка самая низкая. Однако, следует отметить, что если первые три ответа оценивались на уровне «знание» таксономии Блума, то четвертый – на уровне «понимание». Такое смешение подходов к оцениванию недопустимо. Четвертый ответ необходимо переработать и перевести его на уровень «знание».
Четвертый ответ самый длинный и это важно, так как он является дистрактором. Если в задании есть очень короткие и очень длинные ответы, то следует избегать ситуации, когда эти, бросающиеся в глаза, ответы были верными. Чаще всего испытуемые, не зная верного ответа, пытаясь угадать, выбирают самый длинный.
Принцип кумуляции можно использовать и в скрытом виде.
Пример № 32.
УКАЖИТЕ ЧЕТЫРЕ ФИЗИЧЕСКИХ ЯВЛЕНИЯ16
1) таяние снега, дождь, радуга, метель
2) таяние снега, дождь, землетрясение, почернение серебряной монеты
3) таяние снега, скисание молока, гниение соломы, закат солнца
4) скисание молока, гниение соломы, почернение серебряной монеты,
растворение соли в воде
Это задание также позволяет однозначно оценить ответы, так как имеется удобный числовой параметр – количество физических явлений, упомянутых в ответе. В первом ответе все четыре явления – физические, оценка «5». Во 2-м ответе три явления физические, одно – химическое, оценка «4». В 3-м ответе два – физические, два – химические, оценка «3». В 4-м ответе физических явлений нет, оценка «2».
Теперь обратимся к проблеме оценивания ответа испытуемого.
По нашему мнению, конструирование заданий с градуированными ответами с четким критерием оценивания ответов является сложной задачей, требующей немалого искусства от составителя. По этой причине лучше использовать градуированные задания с уменьшенным количеством градаций правильности ответов, например, только «5» и «2». Иными словами, среди предложенных есть несколько совершенно верных и несколько совершенно неверных ответов. В этом случае требования к критерию оценивания значительно ослабляются и задание составить гораздо легче. Легко видеть, что тогда задание с градуированными ответами превращается в задание с выбором нескольких правильных ответов.
Рассмотрим процедуру оценивания заданий с градуированными ответами. Как отмечалось в первой главе, технология мягкого (soft testing), непрямого тестирования развивается И.А.Моревым17, под руководством которого разработано программное средство для ЭВМ - «STEACHER». Эта компьютерная программа позволяет осуществить тестирование в форме дидактической игры. Для оценивания заданий с градуированными ответами И.А.Морев вычсляет скалярный рейтинг
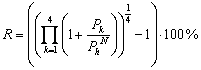
где h - нумерует уровни ответов, PhN - нормативный показатель уровня h.
Для полноты расчетов необходима еще оценочная таблица, кроме того, нормативный показатель в некоторых случаях оказывается отрицательным, что лишено смысла и, поэтому, требуются специальные правила пересчета.
О.Н.Фалалеева18 предлагает другой метод оценивания, в котором вводятся три величины: Х - "номер ответа", Y - "оценка ответа", Z - "номер тестового задания". Величины X, Y представляют собой распределение оценок по ответам на Z-вое тестовое задание. На рис.2.9.1 показано такое распределение для одного из заданий. Здесь по оси ординат отложены значения Y, а по оси абсцисс – X.. Кружочки соответствуют "истинным оценкам", выставленным экспертами в данной предметной области; треугольниками - оценки, выставленные испытуемым каждому ответу данного тестового задания.
Необходимо оценить эту совокупность (множество) оценок испытуемого. Оценивание зависит от величины отклонения DY в плоскости XY (рис.2.9.1).
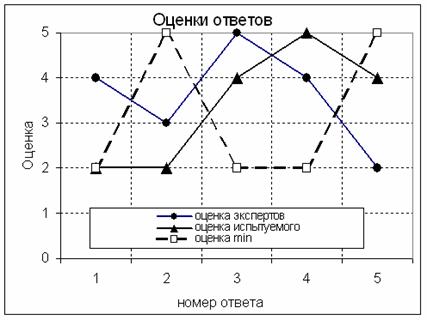
Рис.2.9.1. Оценивание заданий с градуированными ответами.
При нулевой разности всех ординат DY=0 испытуемый получит наивысшую оценку "5". На практике, конечно, суммарная разность ординат вероятнее всего будет ненулевой. В этом случае необходимо вычислить относительную долю суммарного отклонения. Для этого необходимо знать максимально возможное отклонение. В качестве максимального отклонения оценки k -го ответа возьмем наибольшую из двух величин (a и b) - расстояние между "истинным" ответом и максимальной или минимальной оценками. В частности , Ymax="5" , Ymin="2" . Очевидно, что Ymin+ a + b = Ymax. Нас интересует только сдвиг DY= a + b, поэтому абсолютные значения Ymin и Ymax.не имеют значения. Суммарное отклонение для z-го задания будет равно
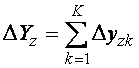
где k - номер ответа, K - количество ответов в данном тестовом задании.
В нашем примере K=5. Теперь найдем DYmax - максимальное отклонение для данного тестового задания. Ясно, что эта величина будет различной для разных тестовых заданий. Величина DYmax будет складываться из максимальных отклонений для каждой оценки.
В нашем случае, например, для первого ответа DYz1=4-2=2 и DYz max = 2+2+3+2+3=12.
Теперь найдем текущее отклонение:
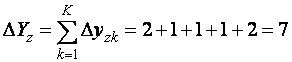
или в относительных единицах (степень отклонения)
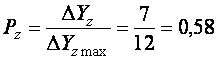
Удобнее пользоваться не степенью отклонения Pz, а степенью совпадения Sz = 1- Pz. = 0,42. Величина Sz характеризует оценку испытуемого за ответ на данное задание.
Таким образом, задания с градуированными ответами, очень привлекательны. Они не подвержены эффекту угадывания, но создать ответы с четкими градациями нелегко. Процедура оценивания довольно громоздкая и требует обязательного использования вычислительной техники.