Создателем классической теории тестов (Classical Theory of mental tests) является
известный британский психолог, автор факторного анализа, Чальз Эдвард Спирмен (Charles Edward Spearman) (1863-
Большой вклад в развитие классической теории тестов внес Льюис Гуттман (Louis Guttman, 1916-1987)3.
Всесторонне и полно классическая теория тестов впервые изложена в
фундаментальном труде Гарольда Гулликсена (Gulliksen H.,
Классическая теория тестов основывается на следующих пяти основных положениях.
1. Эмпирически полученный результат измерения (X) представляет собой сумму истинного результата измерения (T) и ошибки измерения (E)8:
X = T + E (3.1.1)
Величины T и E обычно неизвестны.
2. Истинный результат измерения можно выразить как математическое ожидание E(X):
T = E(X)
3. Корреляция истинных и ошибочных компонентов по множеству испытуемых равна нулю, то есть ρTE = 0.
4. Ошибочные компоненты двух любых тестов не коррелируют:
ρE1,E2 = 0
5. Ошибочные компоненты одного теста не коррелируют с истинными компонентами любого другого теста:
ρE1,T2 = 0
Кроме этого, основу классической теории тестов составляют два определения – параллельных и эквивалентных тестов.
ПАРАЛЛЕЛЬНЫЕ тесты должны соответствовать требованиям (1-5), истинные компоненты одного теста (T1) должны быть равны истинным компонентам другого теста (T2) в каждой выборке испытуемых, отвечающих на оба теста. Предполагается, что T1=T2 и, кроме того, равны дисперсии s12 = s22.
Эквивалентные тесты должны соответствовать всем требованием параллельных тестов за исключением одного: истинные компоненты одного теста не обязательно должны равняться истинным компонентам другого параллельного теста, но отличаться они должны на одну и ту же константу с.
Условие эквивалентности двух тестов записывается в следующем виде:
T1 = T2+c12
где c12 - константа различий результатов первого и второго тестов.
На основе приведенных положений построена теория надежности тестов9,10.
Далее, примем в качестве исходного положения следующее утверждение
![]() (3.1.2)
(3.1.2)
то есть, дисперсия полученных тестовых баллов равна сумме дисперсий истинных и ошибочных компонентов.
Перепишем это выражение в следующем виде:
 (3.1.3)
(3.1.3)
Правая часть этого равенства представляет собой надежность теста (r). Таким образом надежность теста можно записать в виде:
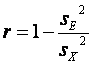 (3.1.4)
(3.1.4)
На основе этой формулы в последующем были предложены различные выражения для нахождения коэффициента надежности теста. Надежность теста представляет собой его важнейшую характеристику. Если неизвестна надежность, то результаты тестирования невозможно интерпретировать. Надежность теста характеризует его точность как измерительного инструмента. Высокая надежность означает высокую повторяемость результатов тестирования в одинаковых условиях.
В классической теории тестов важнейшей проблемой является определение истинного тестового балла испытуемого (T). Эмпирический тестовый балл (X) зависит от многих условий – уровня трудности заданий, уровня подготовленности испытуемых, количества заданий, условий проведения тестирования и т.д. В группе сильных, хорошо подготовленных испытуемых, результаты тестирования будут как правило, лучше,. чем в группе слабо подготовленных испытуемых. В этой связи остается открытым вопрос о величине меры трудности заданий на генеральной совокупности испытуемых. Проблема заключается в том, что реальные эмпирические данные получают на вовсе не случайных выборках испытуемых. Как правило, это учебные группы, представляющие собой множество учащихся достаточно сильно взаимодействующих между собой в процессе учения и обучающиеся в условиях, часто не повторяющихся для других групп.
Найдем sE из уравнения (3.1.4)
![]()
Здесь в явной форме показана зависимость точности измерения от величины стандартного отклонения sX и от надежности теста r.