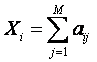
Выполнение статистической обработки результатов тестирования начинается с формирования так называемой матрицы тестовых результатов6.
МАТРИЦА ТЕСТОВЫХ РЕЗУЛЬТАТОВ aij – это матрица размерности NxM, содержащая числовые обозначения градации индикатора, связанного с изучаемой латентной переменной, где M-число индикаторов, N-число испытуемых.
Эта матрица представляет собой таблицу, строки, которой соответствуют испытуемым, а столбцы – индикаторным переменным. В случае тестирования учебных достижений индикаторными переменными являются тестовые задания. На пересечении строк и столбцов находится число, соответствующее ответу данного испытуемого на данное задание.
В политомическом случае ответ испытуемого характеризуется числами в некотором диапазоне, например от нуля до девяти. Допустим, 0 соответствует полному отсутствию знаний, а 9 – наличию полных знаний для данного тестового задания. Промежуточные варианты описываются числами* в диапазоне от 0 до 9. Пример политомической матрицы результатов тестирования приведен в таблице 3.2.1.
Таблица 3.2.1. Политомическая матрица результатов тестирования
|
№ |
Испытуемые |
Номера заданий |
||
|
1 |
2 |
3 |
||
|
1 |
Иванов |
3 |
4 |
0 |
|
2 |
Сидоров |
5 |
8 |
4 |
|
3 |
Петров |
9 |
8 |
5 |
|
4 |
Алексеев |
6 |
5 |
3 |
|
5 |
Михайлов |
8 |
7 |
0 |
Отметим, что числа, расположенные в ячейках таблицы, отсчитываются по порядковой шкале (см. главу 1). Рассмотрим, например, задание №1. Числа в политомической матрице показывают, что с первым заданием испытуемые справились с различным успехом. В порядке убывания их можно ранжировать: Петров (9), Михайлов (8), Алексеев (6), Сидоров (5), Иванов (3). С этими цифрами нельзя производить арифметические операции – складывать, вычитать, умножать, делить (см. главу 1). Это происходит оттого, что цифры от 0 до 9 являются не числами, а упорядоченными символами для описания градации знаний испытуемых, то есть, эти символы (0-9) размещены на порядковой шкале.
Матрица состоит векторов-строк, содержащих значения индикатора для испытуемого. Матрицу можно упорядочить как по строкам, так и по столбцам.
ПРОФИЛЬ ИСПЫТУЕМОГО – это последовательность значений индикатора в упорядоченной матрице тестовых результатов.
В дихотомическом случае ответы испытуемого характеризуется двумя символами (цифрами) - 0 и 1. Нулю соответствует неверный ответ, единице – верный ответ.
На практике чаще всего используется дихотомический случай, поэтому в дальнейшем мы будем рассматривать именно его.
БИНАРНАЯ МАТРИЦА - это матрица результатов тестирования для дихотомического случая. Пример дихотомической матрицы приведен в таблице 3.2.2.
Таблица 3.2.2. Бинарная матрица (11х9).
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1. Иванов |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
|
2. Сидоров |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
|
3. Петров |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
|
4. Алексеев |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
|
5. Михайлов |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|
6. Федоров |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
|
7. Антонов |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
8. Кузнецов |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
|
9. Болдырев |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
|
10. Яковлев |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
|
11. Громов |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
Для дальнейшего анализа, нам потребуются значения Хi - индивидуального балла i-го испытуемого, количество верных ответов Rj, на j-е задание, количество неверных ответов Wj на j-е задание, доля верных ответов pj и доля неверных ответов qj.
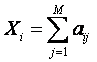
В нашем случае (M=9) индивидуальный тестовый балл, например, для второго испытуемого (i=2) равен:
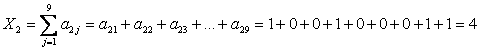
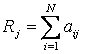
![]()
В нашем случае (N=11) для третьего задания ( j=3 ) получаем:
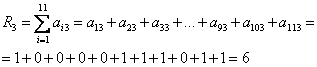
W3=11-R3 = 11-6=5
Доля верных ответов pj на j-е задание равна:
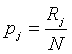
Параметр pj принято называть мерой трудности задания, хотя логично было бы называть его мерой легкости тестового задания.
Доля неверных ответов равна qj = 1 - pj.
В нашем случае для третьего задания получим:
![]()
q3 = 1 – p3 = 1 – 0.545 = 0.455
В таблице 3.2.3 приведены вычисленные значения Xi и Rj. Для удобства визуального анализа ячейки с нулевыми значениями заштрихованы. В отличие от предыдущей таблицы, здесь фамилии испытуемых заменены их номерами. Крайний правый столбец содержит значения индивидуальных тестовых баллов испытуемых Xi. Самая нижняя строка содержит количество правильных ответов на задания Rj. Для удобства визуального контроля, ячейки с нулевыми значениями заштрихованы.
Таблица 3.2.3. Бинарная матрица (11х9) с индивидуальными тестовыми баллами испытуемых.
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
Xi |
|
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
5 |
|
2 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
3 |
|
3 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
2 |
|
4 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
4 |
|
5 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
3 |
|
6 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
6 |
|
7 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
9 |
|
8 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
7 |
|
9 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
2 |
|
10 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
7 |
|
11 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
8 |
|
Rj |
6 |
3 |
6 |
2 |
7 |
5 |
8 |
11 |
8 |
56 |
Далее, необходимо упорядочить бинарную матрицу. Сначала выполним упорядочение по величине Xi. Для этого строки с большими значениями Xi переместим вверх, с меньшими значениями - вниз. В результате, строка №7 передвинулась на самый верх, а строка №9 - вниз. Аналогично выполняется упорядочение по значению Rj. В этом случае перемещаются столбцы. Столбец №8 становится крайним левым, а №4 - крайним правым (таблица 3.2.4).
Отметим, что после упорядочения, нумерация строк и столбцов нарушилась. Столбец №8 является первым, №7 - вторым, №9 - третьим и т.д. Номера столбцов сохранены именно такими, какими были номера заданий в тесте. Это важно для установления взаимно однозначного соответствия между заданиями в упорядоченной и исходной матрицах. Это же самое относится и номерам строк (испытуемых).
Таблица 3.2.4. Бинарная матрица (11х9), упорядоченная по Xi и по Rj
|
|
8 |
7 |
9 |
5 |
1 |
3 |
6 |
2 |
4 |
Xi |
|
7 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
9 |
|
11 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
8 |
|
8 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
7 |
|
10 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
7 |
|
6 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
6 |
|
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
5 |
|
4 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
4 |
|
2 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
3 |
|
5 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
3 |
|
3 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
2 |
|
9 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
|
Rj |
11 |
8 |
8 |
7 |
6 |
6 |
5 |
3 |
2 |
56 |
Из полученной таблицы видно, что задание №8 успешно выполнили все 11 испытуемых. Это задание не позволяет дифференцировать испытуемых, поэтому его следует удалить из теста. Отметим, что это требование относится только к нормативно-ориентированным тестам. Соответственно, если бы на какое-то задание не ответил ни один испытуемый (Rj=0), то это задание тоже должно быть удалено из теста. Кроме того, испытуемый №7 успешно выполнил все задания теста. Тест не дает информации об испытуемом, за исключением того, что для него все задания слишком легкие. Строку №7 также следует удалить из матрицы.
После удаления столбца №8 и строки №7 мы получим редуцированную бинарную матрицу (таблица 3.2.5).
В этой таблице для удобства добавлена новая нумерация строк и столбцов. В нижней части таблицы приведены значения Rj, Wj, pj, qj, и pj qj.
Важным параметром тестового задания является вариация (дисперсия) тестовых баллов pj qj. Чем больше вариация, тем лучше задание дифференцирует испытуемых.
На рис.3.2.1. показана зависимость вариации тестовых баллов от трудности задания. Видно, что максимальное значение, равное 0,25 достигается при pj = 0,5. При pj = 0 и pj = 1 дисперсия задания равна нулю. Иными словами, если на задание не ответил ни один испытуемый или успешно ответили все, то задание не может их дифференцировать по уровню подготовленности.
Таблица 3.2.5. Редуцированная бинарная матрица 10х8.
|
№ |
новые |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
|
новые |
старые |
7 |
9 |
5 |
1 |
3 |
6 |
2 |
4 |
Xi |
Xi2 |
|
1 |
11 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
7 |
49 |
|
2 |
8 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
6 |
36 |
|
3 |
10 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
6 |
36 |
|
4 |
6 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
5 |
25 |
|
5 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
4 |
16 |
|
6 |
4 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
3 |
9 |
|
7 |
2 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
2 |
4 |
|
8 |
5 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
2 |
4 |
|
9 |
3 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
|
10 |
9 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
|
Rj |
7 |
7 |
6 |
5 |
5 |
4 |
2 |
1 |
37 |
181 |
|
|
Wj |
3 |
3 |
4 |
5 |
5 |
6 |
8 |
9 |
|
|
|
|
pj |
0,7 |
0,7 |
0,6 |
0,5 |
0,5 |
0,4 |
0,2 |
0,1 |
|
|
|
|
qj |
0,3 |
0,3 |
0,4 |
0,5 |
0,5 |
0,6 |
0,8 |
0,9 |
|
|
|
|
pj qj |
0,21 |
0,21 |
0,24 |
0,25 |
0,25 |
0,24 |
0,16 |
0,09 |
|
|
Бинарная матрица (таблица 3.2.5) имеет характерную особенность - почти все нули и единицы распределились относительно диагонали, идущей из левого нижнего угла в правый верхний.
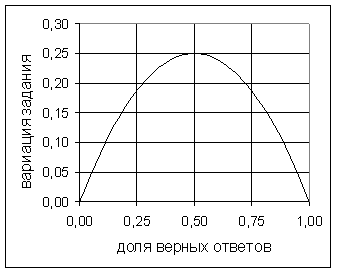
Рис.3.2.1. Вариация задания.
Согласно Гуттману это разграничение должно быть идеальным. Если испытуемый, верно ответил на трудное задание, то он тем более, должен справиться с более легкими заданиями. Это должно приводить к строгому разграничению единиц и нулей диагональю матрицы.
В действительности же это не совсем так. Например, в нашей бинарной матрице профиль испытуемого №2 (№8 по старой нумерации) сильно отклоняется от правила Гуттмана. Этот испытуемый справился с самым трудным заданием №8 (№4 по старой нумерации), но не справился с более легкими заданиями №7 и №3. Профиль испытуемого искажен. Если бы единицы и нули поменялись местами, то есть испытуемый, верно ответил на трудные вопросы, но не справился с легкими, то говорят, у него инвертированный профиль.
Инвертированный профиль свидетельствует либо о неверной структуре знаний испытуемого, либо о нарушении процедуры тестирования (списывание, угадывание и т.д.), либо о недостатках тестовых заданий (по форме и (или) по содержанию.
* Точнее - цифрами. Цифры, числа, состоящие из цифр, в нашем случае это просто упорядоченное множество, каждый элемент которого, обозначен некоторыми символами, например числами (цифрами, если количество элементов не более 10).