Данные, представленные в таблице 3.2.5 удобно анализировать, используя их графическое представление. Для этого надо найти частоты тестовых баллов.
ЧАСТОТА ТЕСТОВОГО БАЛЛА - это количество испытуемых, имеющих данный тестовый балл.
Таблица 3.3.1. Частоты тестовых баллов.
|
Xi |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Частота |
2 |
2 |
1 |
1 |
1 |
2 |
1 |
Эта таблица построена следующим образом. В первой строке приведены все возможные значения индивидуальных баллов испытуемых. Во второй строке указаны частоты индивидуальных баллов. Например, тестовый балл (таблица 3.2.5) равный 1 имеют 2 испытуемых - №3 и №9 (по старой нумерации строк); 2 балла имеют также 2 испытуемых - №2 и №5; 3 балла - 1 испытуемый - №4; 4 балла - 1 испытуемый - №1; 5 баллов - 1 (№6); 6 баллов - 2 (№8 и №10); 7 баллов - 1 (№11).
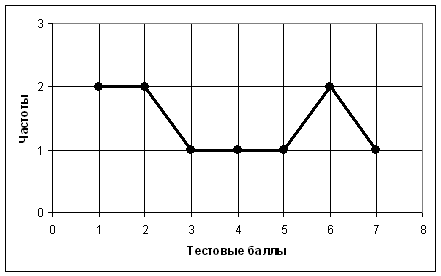
На основании таблицы частот можно построить полигон частот (рис.3.3.1). По оси абсцисс отложены тестовые баллы, а по оси ординат - соответствующие частоты.

Рис.3.3.1. Полигон частот.
Вместо полигона частот иногда используют сглаженную кривую, проходящую максимально близко к экспериментальным точкам (рис.3.3.2).
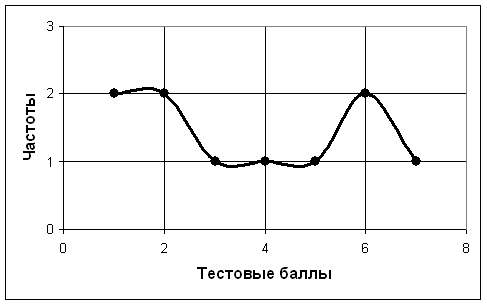
Рис.3.3.2. Сглаженная эмпирическая кривая.
Для графического представления данных можно также использовать гистограммы (рис.3.3.3).

Рис.3.3.3. Гистограмма частот тестовых баллов.
Желательно, чтобы распределение частот тестовых баллов было близко к нормальному (Гауссовому).